APLIKASI TURUNAN (MATEMATIKA)

Selamat datang diblog saya.

Artikel saya kali ini akan membahas tentang aplikasi turunan (matematika).

Apa sih aplikasi turunan?

baiklah saya akan jabarkan secara detail tentang aplikasi turunan (matematika).

Aplikasi Turunan terbagi menjadi 2 yaitu :

1. GARIS SINGGUNG

2. MAKSIMISASI ATAU MINIMISASI

kita akan membahasa satu persatu dan kita akan mulai dari yang pertama yaitu garis singgung

      1. GARIS SINGGUNG

Materi turunan dalam Matematika memiliki sub bab mengenai persamaan garis singgung suatu kurva, maka materi ini pasti akan di temui jika sedang mengulas mengenai turunan. Sebelum kita belajar ke materi inti yaitu cara mencari persamaan garis singgung kurva, kita harus tahu dulu mengenai gradien garis yang disimbolkan dengan m, dimana : 

• gradian garis untuk persamaan y=mx+c adalah m
• gradien garis untuk persamaan ax+by=c, maka m=-a/b
• gradien garis jika diketahui dua titik, misal (x1,y1) dan (x2,y2) maka untuk mencari gradien garisnya m=(y2-y1)/(x2-x1) 

dan untuk gradien dua garis lurus berlaku ketentuan :

• jika saling sejajar maka m1 = m2
• jika saling tegak lurus maka m1.m2 = -1 atau m1 = -1/(m2)

PERSAMAAN GARIS SINGGUNG KURVA

Jika terdapat kurva y = f(x) disinggung oleh sebuah garis di titik (x1, y1) maka gradien garis singgung tersebut bisa dinyatakan dengan m = f'(x1). Sementara itu x1 dan y1 memiliki hubungan y1 = f(x1). Sehingga persamaan garis singgungnya bisa dinyatakan dengan y – y1 = m(x – x1). Jadi intinya jika kita akan mencari persamaan garis singgung suatu kurva jika diketahui gradiennya m dan menyinggung di titik (x1,y1) maka kita gunakan persamaan

                     y - y1 = m (x - x1)

Sedangkan jika diketahui 2 titik, misalnya (x1,y1) dan (x2,y2) maka untuk mencari persamaan garis singgung dari dua titik tersebut kita dapat gunakan persamaan

Agar kalian lebih memahami materi persamaan garis singgung tersebut, perhatikan beberapa contoh soal berikut ini :

untuk pembahasan tentang garis singgung saya rasa cukup sampai disini dan kita akan memasuki pembahasan tentang maksimisasi atau minimisasi.


      2. MAKSIMISASI ATAU MINIMISASI

Pengertian dan persyaratan Global maximum atau Global minimum, Relative maximum atau Relative minimum : Dengan fungsi dari 1 (satu) independent variable y = f (x)

Dependent variable dari fungsi merupakan the objective function yaitu obyek dari maksimisasi (maximization) atau minimisasi (minimization). Maximization atau minimization menetapkan angka atau bilangan dari independent variables sehingga diperoleh angka atau nilai the objective function atau dependent variable tertinggi (maximum) atau terendah (minimum). Karena itu, independent variables juga disebut sebagai choice variables.

Istilah : 

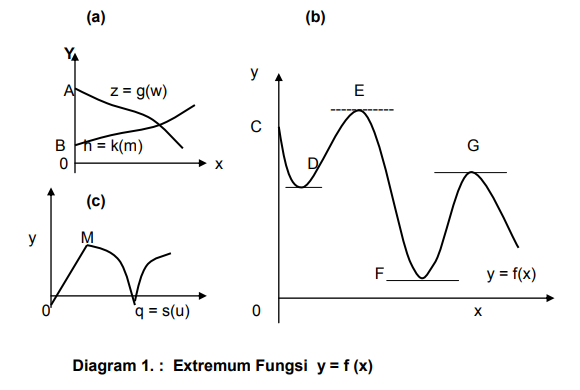
• Baik global maximum atau minimum, maupun relative maximum atau minimum, disebut EXTREMUM (diagram dibawah).

• Titik extremum disebut stationary point. Sedangkan angka atau nilai extremum dari fungsi atau dependent variable atau the objective function disebut a critical value atau stationary value. Selain itu, the slope dari the objective function pada titik extremum adalah 0 (nol).

• Global (absolute) maximum adalah titik atau angka tertinggi dari the objective function atau dependent variable. Contoh, titik A pada fungsi z = g(w) di Diagram 1. (a) di atas.

• Sedangkan, global (absolute) minimum merupakan titik atau angka terendah. Contoh titik B pada fungsi h = k(m) di Diagram 1. (a) atas.

• Relative (local) maximum adalah titik atau angka maximum di sekitar titik itu pada the objective function. Sedangkan, relative (local) minimum adalah titik atau angka minimum di sekitar titik itu pada the objective function. 

Diantara 4 extremums pada diagram 1. (b) di atas, maka :

• Titik E adalah a global (absolute or free) maximum, sedangkan titik G adalah local (relative) maximum. 

• Titik F adalah a global minimum, sedangkan titk D adalah local minimum.

Persyaratan untuk extremum dan inflection point : Dengan fungsi dari 1 (satu) independent variable) y = f (x) 

Catatan :

• Titik M dan N pada Diagram 1.(c) di atas, tidak dapat dianggap extremum karena pada kedua titik itu fungsi g = s(u) tidak kontinyu sehingga tidak terdapat derivatif dari fungsi g.

• Titik infleksi (inflection point) adalah titik dimana tidak terdapat extremum (maximum atau minimum).

Penjelasan inflection point :

• Pada diagram di atas, titik J dan K disebut inflection point karena tanda slope tidak berubah dari sebelum ke sesudah titik J atau K :

• Pada digaram 2.(a), walaupun mempunyai fungsi f(x) derivatif pada titik J = 0 atau f ∕ = 0, yang juga digambarkan dengan slope pada titik J∕ = 0. Tetapi tanda slope atau derivatif f∕ tetap sama positif (slope +) baik sebelum dan sesudah titik J dan J∕ . Padahal syarat titik J menjadi extremum, apabila tanda slope berubah dari sebelum ke sesudah titik extremum J. Apabila titik J minimum, maka tanda slope berubah dari negatif untuk sebelum titik J menjadi positif untuk setelah titik J. Atau sebaliknya, apabila titik J.

• Pada Diagram 2. (b) di atas, derivatif atau slope fungsi g(x) pada titik K tertinggi maximum (tidak sama dengan 0 (nol)) seperti terlihat pada titik K∕ . Tetapi slope atau derivatif atau f∕ sebelum titik K naik (+) tajam dan setelah titik K tetap naik (+) tetapi dengan melandai atau menurun.

baiklah sampai disini dulu pembahasan kita kali ini tentang aplikasi turunan, jika kalian sudah mengerti tentang pembahasan diatas jangan lupa untuk mengshare blog ini keteman-teman kalia supaya bisa bermanfaat buat kita semua. terima kasih