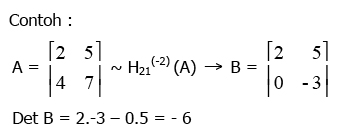MATRIKS LANJUTAN 2 (MATEMATIKA)

Selamat datang kembali di blog saya

Semoga kalian masih semangat untuk mempelajari lebih dalam tentang MATRIKS, ya pembahasan saya kali ini tentang MATRIKS LANJUTAN 2 ini adalah sambungan pembahasan kita minggu lalu.
Sebelum kita memasuki materi pembahasan tersebut saya ingin menjabarkan terlebih dahulu materi pembahasan kita sekarang ini tentang MATRIKS LANJUTAN 2 yang terdiri dari :
1. Determinan Matriks Ordo 3x3
2. Invers Matriks
dan saya juga akan membuatkan contoh dari masing materi diatas supaya kalian lebih cepat memahimi pembahasan kita kali ini.

Oke langsung saja saya mulai dari pembahasan materi yang pertama dari MATRIKS LANJUTAN 2 yaitu tentang Determinan Matriks Ordo 3x3.

Determinan Matriks Ordo 3x3
Pada Matriks ordo 3x3 untuk mencari determinannya terbagi dalam dua metode yaitu :
1. Metode Sarrus
2. Metode Minor dan Kofaktor

1. Metode Sarrus

Contoh soal :

2. Metode Minor dan Kofaktor

Dapat dibentuk suatu sub determinan dari matriks yang disebut sebagai minor. Sehingga Minor |Mij| adalah determinan dari submatriks yang dibentuk dengan menghapus baris ke-i dan kolom ke-j dari matriks tersebut. Dimana |M11| adalah minor dari a11; |M12| adalah minor dari a12 dan |M13| adalah minor dari a13, dan seterusnya.

Apabila suatu minor diberi tambahan tanda (-1)^i+j, maka disebut kofator |Cij|.
Maka |Cij| = (-1)^i+j|Mij|; jika jumlah i+j genap maka akan sama dengan 1. Sedangkan jika jumlah i+j adalah ganjil maka |Cij|=-|Mij|, karena jika (-1) dipangkatkan dengan bilangan negatif maka hasilnya akan sama dengan (-1).

Invers Matriks
1 Mencari Invers dengan Matriks Adjoint
Inverse Matriks (matriks balikan) A-1 hanya dapat ditemukan pada suatu matriks bujur sangkar, dan non singular. Dimana harus memenuhi suatu hubungan sebagai berikut :




Dimana rumus untuk memperolah balikan dari matriks adalah :

2.Mencari Invers dengan transformasi Elementer
Misalnya ada suatu Matriks, Matriks A, dengan rank r, dengan transformasi elementer dapat diubah bentuknya menjadi matriks yang disebut matriks normal.



Untuk mengubah matriks A menjadi matriks normal maka diusahakan mengubah elemen dibawah diagonal a11, a22 dan a33menjadi nol dengan transformasi elemen baris. Dilanjutkan dengan transformasi kolom agar elemen-elemen diatas diagonal tersebut menjadi 0.

Baiklah bro and sis sekian dulu pembahasan kita kali ini tentang MATRIKS LANJUTAN 2 semoga blog ini bisa membantu kalian dalam kesulitan belajar matematika.
jika kalian merasa terbantu dengan blog ini jangan lupa di share ke temen-temen kalian ya bro and sis
terima kasih.

MATRIKS LANJUTAN 1 (MATEMATIKA)

Selamat datang kembali di blog saya

Semoga kalian masih semangat untuk mempelajari lebih dalam tentang MATRIKS, ya pembahasan saya kali ini tentang MATRIKS LANJUTAN 1 ini adalah sambungan pembahasan kita minggu lalu.
Sebelum kita memasuki materi pembahasan tersebut saya ingin menjabarkan terlebih dahulu materi pembahasan kita sekarang ini tentang MATRIKS LANJUTAN 1 yang terdiri dari :
1. Transformasi elementer pada Baris
2. Transformasi elementer pada Kolom
3. Matriks Ekivalen
4. Rank Matriks
5. Pengenalan Konsep Determinan
dan saya juga akan membuatkan contoh dari masing materi diatas supaya kalian lebih cepat memahimi pembahasan kita kali ini.

Oke langsung saja saya mulai dari pembahasan materi yang pertama dari MATRIKS LANJUTAN 1 yaitu tentang Transformasi elementer pada Baris.

Transformasi Elementer pada Baris
Terhadap elemen-elemen suatu matriks dapat dilakukan transformasi atau penukaran atau perpindahan menurut baris matriks.

Kaidah-kaidah transformasi elementer : 
Apabila ada matriks A = (aij), maka transformasi elemen-elemen pada baris ke-i dengan baris ke-j ditulis Hij (A), yang merupakan penukaran semua elemen baris ke-i dengan baris ke-j atau baris ke-j dijadikan baris ke-i.

Contoh : 

setelah saya selesai dengan pembahasan tentangn transformasi elementer pada baris sekarang waktunya kita masuk ke pembahasan tentang transformasi elementer pada kolom.
 
Transformasi Elementer pada Kolom
Terhadap elemen-elemen suatu matriks dapat dilakukan transformasi atau penukaran atau perpindahan menurut kolom matriks.

Transformasi elemen-elemen pada kolom ke-i dengan kolom ke-j, ditulis Kij (A), adalah penukaran semua elemen kolom ke-i dengan kolom ke-j atau kolom ke-i dijadikan kolom ke-j.

 baiklah sekarang kita memasuki pembahasan tentang Matriks Ekivalen.

Matriks Ekivalen
Dua matriks A dan B disebut ekivalen, ditulis A ∼ B, jika B diperoleh dari A dengan melakukan transformasi elementer, dan sebaliknya A diperoleh dari B dengan melakukan invers transformasi elementer. 

Contoh :

dan kita langsung lanjut ke pembahasan berikutnya yaitu tentang Rank Matriks. 


Rank Matriks
Rank baris dari matriks A adalah dimensi dari ruang baris matriks A. Rank kolom dari matriks A adalah dimensi dari ruang kolom matriks A. Bila rank baris = rank kolom maka rank matriks A yaitu r (A) adalah harga atau nilai dari rank baris/ rank kolom matriks A tersebut.
Dengan kata lain rank dari matriks menyatakan jumlah maksimum vektor-vektor baris/kolom yang bebas linear. Untuk mencari rank matriks dapat dilakukan dengan transformasi elementer, yaitu dengan cara sebanyak mungkin mengubah baris kolom menjadi vektor nol.

Contoh :

  
Petunjuk menentukan rank matriks :
i. Bila matriks hanya mempunyai dua baris, maka cukup diperiksa apakah elemen-elemen pada baris ke-1 dan baris ke-2 saling berkelipatan. 

Contoh : 

  ii. Secara umum :

1. Pilih baris / kolom yang bukan vektor nol, dan pilih elemen pada baris/kolom tersebut yang tidak sama dengan nol sebagai elemen pivot. Pada contoh transformasi baris a13 =1 (≠ 0), kemudian pilih baris yang mengandung elemen 1 atau –1 sebagai elemen pivot.
2. Jadikan nol semua elemen yang sekolom dengan elemen pivot melalui transformasi baris oleh elemen pivot tersebut. Pada contoh diatas a23, a33 dan a43 dijadikan nol.
3. Selanjutnya tidak perlu lagi memeperhatikan baris pivot diatas. Perhatikan baris-baris yang tinggal. Pada contoh diatas adalah baris. Kerjakan langkah (1) terhadap mereka. Pada contoh diatas pilih baris 4 dengan elemen pivot a41=1. Seterusnya kembali lagi pada langkah a dan b.
4. Proses ini akan berakhir bila langkah a tidak dapat dikerjakan lagi, yaitu bila telah menjadi baris nol. 

okeeey lanjut kita akan membahas lebih dalam tentang DETERMINAN, kita akan bahas lebih dalam lagi mulai dari pengertian determian, sifat-sifat determian dan ekspansi laplace.


Determinan
Pengertian determinan :
Determinan merupakan sebuah bilangan tunggal atau scalar, dan hanya dijumpai dalam matriks bujur sangkar. Jika determinan suatu matriks bujur sangkar adalah nol, maka matriks tersebut dikatakan sebagai matriks singular. Dan jika determinan matriks tersebut bukan nol, maka matriks tersebut dikatakan sebagai matriks non singular. Matriks nonsingular, secara linear tidak tergantung (saling independent)

Determinan Matriks Ordo 2 x 2
Jika diberikan matriks ordo 2 dinyatakan seperti bentuk di bawah. 

Sifat-sifat Determinan :
Sifat-sifat determinan ada enam, yaitu :
 a. Determinan suatu matriks sama dengan determinan dari transposenya, det (A) = det (A^t).

Contoh :

 b. Penambahan atau pengurangan suatu kelipatan bukan nol dari suatu baris/kolom dari baris/kolom lainnya tidak akan mempunyai pengaruh pada determinan.  

 c. Penukaran tempat antara dua baris atau kolom sembarang dari suatu matriks akan merubah tanda, tetapi tidak merubah harga absolut dari determinan.

Contoh :

  d. Determinan dari suatu matriks segitiga (triangular matriks), yaitu matriks dengan elemen-elemen nol diatas atau di bawah diagonal utama, adalah sama dengan hasil kali dari elemenelemen dari diagonal utama.

Contoh :

  e. Jika semua elemen dari suatu baris atau kolom adalah nol, determinan adalah nol.

Contoh :

 
  f. Jika dua baris atau kolom identik, atau proporsional, yaitu secara linear tergantung, maka determinan adalah nol.

Contoh :

Ekspansi Laplace
Metode atau ekspansi Laplace adalah suatu cara untuk menghitung determinan dengan menggunakan kofaktor.
Determinan dari suatu matriks = jumlah perkalian elemen-elemen dari sembarang baris/kolom dengan kofaktor-kofaktornya.

Ekspansi Laplace dapat ditulis dengan cara :

|A| = a11|C11|+a12|C12|+a13|C13| menggunakan baris 1
 
Dengan pola yang sama dapat juga dihitung dengan menggunakan baris ke dua dan ketiga, dengan memberikan hasil determinan yang sama.

Baiklah bro and sis sekian dulu pembahasan kita kali ini tentang MATRIKS LANJUTAN 1 semoga blog ini bisa membantu kalian dalam kesulitan belajar matematika.
jika kalian merasa terbantu dengan blog ini jangan lupa di share ke temen-temen kalian ya bro and sis
terima kasih.

KUPAS TUNTAS MATRIKS (MATEMATIKA)

Welcome back to my blog bro and sis

Kali ini saya ingin menulis artikel tentang dasar-dasar martriks, buat kalian yg mau tau lebih lanjut tentang dasar-dasar matriks saya akan jabarkan satu persatu mulai dari pengertian matriks, operasi matriks, dan juga saya akan berikan contoh soal untuk pembelajaran kalian semua bro and sis.

Kita langsung mulai dari pengertian matriks, apa itu pengertian matriks?

Pengertian Matriks 

Pengertian Matriks adalah susunan bilangan-bilangan riil atau kompleks yang diatur dalam baris-baris dan kolom-kolom berbentuk persegi panjang. Bilangan-bilangan tersebut disebut elemen matriks. Cara penulisan kolom matriks adalah sebagai berikut (dengan angka) :

Matriks dinyatakan dalam huruf besar A, B, P atau huruf yang lainnya. Atau secara lengkap ditulis A = (aij), artinya matriks A mempunyai elemen aij, dimana indeks i menyatakan baris ke-i dan indeks j menyatakan kolom ke-j dari elemen aij. Secara umum, matriks A ditulis : A = (aij)

Matriks A mempunyai baris sebanyak n dan kolom sebanyak m. Pada matriks A = (amxn), dikatakan ordo matriks A adalah m x n.

Contoh Matriks A mempunyai ordo 2x2.

Contoh Matriks B mempunyai ordo 2x3.

Contoh Matriks C mempunyai ordo 5x1.

Apabila Matriks A dan matriks B berordo sama, dan aij = bij untuk semua i=1,2,..,n dan j=1,2,..m maka matriks tersebut sama.
Contoh :

setelah kita selesai dengan pembahasan diatas tentang pengertian matriks. Sekarang kita lanjut ke pembahasan berikutnya yaitu Operasi Matriks.
Operasi Matriks terbagi dalam beberapa jenis, yaitu :

• Penjumlahan dan pengunrangan
• Perkalian skalar/bilangan dengan matriks
• Transpose Matriks
• Perkalian antar Matriks
• Jenis - jenis Matriks

Operasi Matriks

Dalam operasi matriks terdapat beberapa sifat matriks jika matriks A, B dan C berordo sama dan scalar, maka berlaku sifat-sifat berikut:

1. Operasi penjumlahan dan pengurangan

Jumlah matriks A dan B jika ditulis A + B adalah sebuah matriks baru C, C = A + B dengan elemen Cij = aij +bij, i = 1,2,…,m dan j = 1,2,…,n dengan syarat A dan B mempunyai ordo sama. Jadi matriks C = (cij) = (aij + bij).

Contoh Operasi Penjumlahan :

Contoh Operasa Pengurangan :

4. Operasi Perkalian

Bila A = (aij) berorodo (pxq) dan matriks B = (bij) berordo (qxr), maka perkalian matriks A dan B ditulis AxB, adalah matriks C = AxB = (cij) berordo (pxr), dimana cij = a11bij + a12b2j+..….+ a1qbqr Syarat agar matriks A dan B bisa dikalikan adalah banyaknya kolom matriks A harus sama dengan banyaknya baris matriks B.

Contoh :

5. Jenis-jenis Matriks

i. Matriks bujur sangkar, apabila suatu matriks memiliki jumlah baris dan kolom sama, atau berordo nxn.

Contoh :

ii. Matriks nol, adalah matriks yang semua elemennya sama dengan nol.

Contoh :

iii. Matriks diagonal, adalah matriks bujur sangkar yang semua elemen diluar diagonal utama sama dengan nol.

Contoh :

iv. Matriks satuan (identitas), ditulis dengan I adalah matriks bujur sangkar yang elemen diagonalnya semua sama dengan 1, dan elemen yang lain sama dengan 0.

Contoh :

vi. Matriks segitiga bawah adalah matriks bujur sangkar yang semua elemen diatas diagonal utama adalah 0.

Contoh :

saya akan kasih contoh soal untuk pembelajarannya ya.

contoh soal :

Baiklah bro and sis sekian dulu pembahasan kita kali ini tentang MATRIKS semoga blog ini bisa membantu kalian untuk mengerjakan tugas kalian.
jika kalian merasa terbantu dengan blog ini jangan lupa di share ke temen-temen kalian ya bro and sis
terima kasih.

APLIKASI TURUNAN (MATEMATIKA)

Selamat datang diblog saya.

Artikel saya kali ini akan membahas tentang aplikasi turunan (matematika).

Apa sih aplikasi turunan?

baiklah saya akan jabarkan secara detail tentang aplikasi turunan (matematika).

Aplikasi Turunan terbagi menjadi 2 yaitu :

1. GARIS SINGGUNG

2. MAKSIMISASI ATAU MINIMISASI

kita akan membahasa satu persatu dan kita akan mulai dari yang pertama yaitu garis singgung

      1. GARIS SINGGUNG

Materi turunan dalam Matematika memiliki sub bab mengenai persamaan garis singgung suatu kurva, maka materi ini pasti akan di temui jika sedang mengulas mengenai turunan. Sebelum kita belajar ke materi inti yaitu cara mencari persamaan garis singgung kurva, kita harus tahu dulu mengenai gradien garis yang disimbolkan dengan m, dimana : 

• gradian garis untuk persamaan y=mx+c adalah m
• gradien garis untuk persamaan ax+by=c, maka m=-a/b
• gradien garis jika diketahui dua titik, misal (x1,y1) dan (x2,y2) maka untuk mencari gradien garisnya m=(y2-y1)/(x2-x1) 

dan untuk gradien dua garis lurus berlaku ketentuan :

• jika saling sejajar maka m1 = m2
• jika saling tegak lurus maka m1.m2 = -1 atau m1 = -1/(m2)

PERSAMAAN GARIS SINGGUNG KURVA

Jika terdapat kurva y = f(x) disinggung oleh sebuah garis di titik (x1, y1) maka gradien garis singgung tersebut bisa dinyatakan dengan m = f'(x1). Sementara itu x1 dan y1 memiliki hubungan y1 = f(x1). Sehingga persamaan garis singgungnya bisa dinyatakan dengan y – y1 = m(x – x1). Jadi intinya jika kita akan mencari persamaan garis singgung suatu kurva jika diketahui gradiennya m dan menyinggung di titik (x1,y1) maka kita gunakan persamaan

                     y - y1 = m (x - x1)

Sedangkan jika diketahui 2 titik, misalnya (x1,y1) dan (x2,y2) maka untuk mencari persamaan garis singgung dari dua titik tersebut kita dapat gunakan persamaan

Agar kalian lebih memahami materi persamaan garis singgung tersebut, perhatikan beberapa contoh soal berikut ini :

untuk pembahasan tentang garis singgung saya rasa cukup sampai disini dan kita akan memasuki pembahasan tentang maksimisasi atau minimisasi.


      2. MAKSIMISASI ATAU MINIMISASI

Pengertian dan persyaratan Global maximum atau Global minimum, Relative maximum atau Relative minimum : Dengan fungsi dari 1 (satu) independent variable y = f (x)

Dependent variable dari fungsi merupakan the objective function yaitu obyek dari maksimisasi (maximization) atau minimisasi (minimization). Maximization atau minimization menetapkan angka atau bilangan dari independent variables sehingga diperoleh angka atau nilai the objective function atau dependent variable tertinggi (maximum) atau terendah (minimum). Karena itu, independent variables juga disebut sebagai choice variables.

Istilah : 

• Baik global maximum atau minimum, maupun relative maximum atau minimum, disebut EXTREMUM (diagram dibawah).

• Titik extremum disebut stationary point. Sedangkan angka atau nilai extremum dari fungsi atau dependent variable atau the objective function disebut a critical value atau stationary value. Selain itu, the slope dari the objective function pada titik extremum adalah 0 (nol).

• Global (absolute) maximum adalah titik atau angka tertinggi dari the objective function atau dependent variable. Contoh, titik A pada fungsi z = g(w) di Diagram 1. (a) di atas.

• Sedangkan, global (absolute) minimum merupakan titik atau angka terendah. Contoh titik B pada fungsi h = k(m) di Diagram 1. (a) atas.

• Relative (local) maximum adalah titik atau angka maximum di sekitar titik itu pada the objective function. Sedangkan, relative (local) minimum adalah titik atau angka minimum di sekitar titik itu pada the objective function. 

Diantara 4 extremums pada diagram 1. (b) di atas, maka :

• Titik E adalah a global (absolute or free) maximum, sedangkan titik G adalah local (relative) maximum. 

• Titik F adalah a global minimum, sedangkan titk D adalah local minimum.

Persyaratan untuk extremum dan inflection point : Dengan fungsi dari 1 (satu) independent variable) y = f (x) 

Catatan :

• Titik M dan N pada Diagram 1.(c) di atas, tidak dapat dianggap extremum karena pada kedua titik itu fungsi g = s(u) tidak kontinyu sehingga tidak terdapat derivatif dari fungsi g.

• Titik infleksi (inflection point) adalah titik dimana tidak terdapat extremum (maximum atau minimum).

Penjelasan inflection point :

• Pada diagram di atas, titik J dan K disebut inflection point karena tanda slope tidak berubah dari sebelum ke sesudah titik J atau K :

• Pada digaram 2.(a), walaupun mempunyai fungsi f(x) derivatif pada titik J = 0 atau f ∕ = 0, yang juga digambarkan dengan slope pada titik J∕ = 0. Tetapi tanda slope atau derivatif f∕ tetap sama positif (slope +) baik sebelum dan sesudah titik J dan J∕ . Padahal syarat titik J menjadi extremum, apabila tanda slope berubah dari sebelum ke sesudah titik extremum J. Apabila titik J minimum, maka tanda slope berubah dari negatif untuk sebelum titik J menjadi positif untuk setelah titik J. Atau sebaliknya, apabila titik J.

• Pada Diagram 2. (b) di atas, derivatif atau slope fungsi g(x) pada titik K tertinggi maximum (tidak sama dengan 0 (nol)) seperti terlihat pada titik K∕ . Tetapi slope atau derivatif atau f∕ sebelum titik K naik (+) tajam dan setelah titik K tetap naik (+) tetapi dengan melandai atau menurun.

baiklah sampai disini dulu pembahasan kita kali ini tentang aplikasi turunan, jika kalian sudah mengerti tentang pembahasan diatas jangan lupa untuk mengshare blog ini keteman-teman kalia supaya bisa bermanfaat buat kita semua. terima kasih